実験的(?)折り紙動画3本
特別良いスペックではないにせよちょっとした動画編集ができる環境にもなったし、講習用に買ったウェブカメラもあるので、なんか折り紙を扱った動画が作れないかなという気持ちでいる。とは言え、前にも書いたようにチュートリアル動画を作るつもりはないし、自分自身をコンテンツにするような方向性(トークとかプレゼンとか)も向いていないと思うので何を作るのかは難しいところだ。
以下の3本は、そんな中で作ってみた一発ネタのような折り紙動画だ。もう2ヶ月以上前にアップしたものだが記事にしておく。
クロマキー折り紙
youtu.be
youtu.be
去年思いつきとしてツイートしたネタなのだけど、誰かやってそうで誰もやってなさそうだったので自分でやってみた。作り方は、背景となるカッターマットをOBSでスクリーンショットを取り、その画像をOBSのウェブカメラのソースの下に配置、そしてウェブカメラの映像にクロマキーの設定を加えて特定の色を抜くようにする、というもの。抜いた範囲から後ろの画像が見えるので、透明のように見える。ウェブカメラの位置がずれてしまうと背景画像から撮り直しになってしまうためそこだけ注意(撮り直した)。
1本目、紙が見えなくなる動画のはじめのひと折りでネタとしてはほぼ消化されるのだけど、手が見えなくなるものも撮ってみた。クロマキー用途のゴム手袋という商品もあるようだが、アレルギーの気があるのでカラー軍手を入手した。薄手とうたっていた商品だったが、物としては普通に軍手なので折り紙をするにはちょっと無理があった。
折り動画ダブミックス
youtu.be
単に録音したトラックにリバーブ(残響)とディレイ(こだま)をかけまくっただけのものをダブミックスと言っていいのかは分からないが、タイトルの最後にdub mixって入ってたら可笑しいなという。要するに「紙を折っている音」を音響的にフィーチャーする試みとして作ってみた。作品を等倍速で折っている映像だけど、手順解説を意図したものではない、というひねくれた動画でもある。
折っている作品は、直前に創作した「こいのぼり」で、紙と指だけで発する音にしたかったので最初から空中で浮かせて折った。音処理をしたGarageBandには動画を読み込む機能もあるので、工程に合わせてエフェクトを細かくエディットしている。
同じように、紙を折っている音にクローズアップしたASMR動画というのは結構あるようだ。またポール・ジャクソンさんは紙の音だけを使った音楽を作っている。これらは逆に電子的な音響処理をしないところが肝かもしれない。
市間いおり新曲「Night Folding」
Night Folding/市間いおり
胸がざわめき 眠れない夜は
紙を手にして 指に心ゆだねる そう
いつから折り紙、好きだったかな。
いつの間にか特別になってた。
もう切り離せない、わたしの一部。
だからこれから探しに行くの。
いま、この世界に存在するのは、
紙と、わたしと、紙の音だけ。
このままきっとどこだって行ける。
このままもっと遠くまで連れてって!
不安抱えて 寝つけない夜は
紙を手にして 指に自分ゆだねる そう
最近はひとに見せることばかり…
どこか窮屈な気持ちで折ってた。
今夜はなんだか、自由な感じ。
どこかゆがんでも、私のかたち。
いま、この世界に存在するのは、
紙と、わたしと、紙の音だけ。
このままきっとどこだって行ける。
このままずっと遠くまで連れてって!
曲がりくねった折り図を辿って、
どんなかたちに出会えるかしら。
まっすぐつけた折り筋の先に、
どんな景色が待ってるかしら。
いま、この世界に存在するのは、
紙と、わたしと、紙の音だけ。
このままきっとどこだって行ける。
このままもっと遠くまで連れてって!
胸がざわめき 眠れない夜は
紙を手にして ひとり心ゆだねる そう
胸がざわめき 眠れない夜は
紙を手にして 指に心ゆだねる そう
今回の目標は、アイドルが歌う「聴いててこそばゆくなるラップ」を再現できないかというものだった。
曲調からタイトルをイメージして、そこから「自分自身のために折る時間」というようなテーマで作詞してみたが、こういうベタな歌詞を書くのは市間いおりというフィルターが無いと恥ずかしい。
ラップ部分は、読んだ感じが自然であればいいから押韻は特に気にしないものとして一気に書いた。文字数の関係で言葉足らずになっているところがあるものの、ところどころでうまいこと韻を踏めたのでまあまあ満足。
「アメリカンコッカースパニエル」
アメリカンコッカースパニエルの折り紙というと『神谷流 創作折り紙に挑戦!』に収録されている神谷哲史さんの作品が有名だろう。同作品は毛をカットした姿を折っていたため、長毛の姿を折ってみたらどうかと考えた。毛の表現は継続的に取り組んでいるテーマだが、この題材を折ってみようと思ったのは数年くらい前のことだ。
最初に浮かんだアイデアは「平行に細かく中割り折りした構造を曲面状に半開折りにする」という、「双曲放物線面」で見るアレをうまく使えないか?という発想だった。予想に難くないが、結果からいうと一枚折りでは紙の厚みの問題から実現が難しいものだった。造形的には面白くなりそうな気配はあるので、切り折り紙的な手法なら形になるかもしれない。
最終的には、バラバラに試作していた顔と胴体のパーツのアイデアを用いて形になったのだが、「パーツそのものがあって、それを繋いだ」というよりは「見立て」を含んだ造形・構造の試作アイデアを適宜変化させつつ再利用するというような感じだった。Twitterで一旦公開した後に耳を改良しているが、これもすでにあった頭部試作の構造は変えてデザインだけを組み入れて形になっている。
ある程度構造がまとまってきた段階で、その構造が以前に記事にした「折り線トポロジー」的な展開ができるものであることに気づいた。つまり犬の見立てを得られるような無限の比率的なバリエーションが存在する。
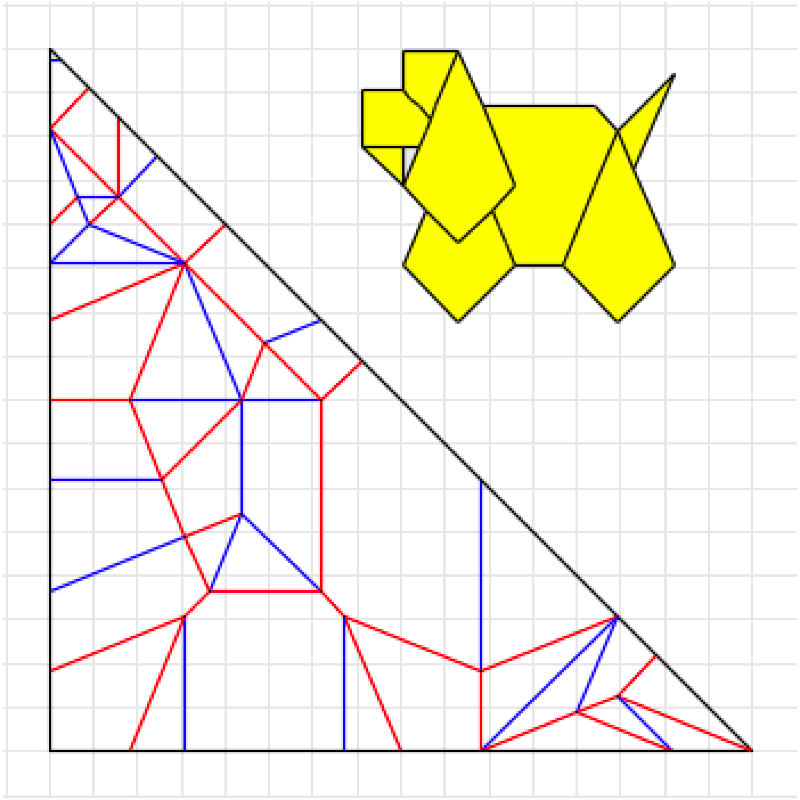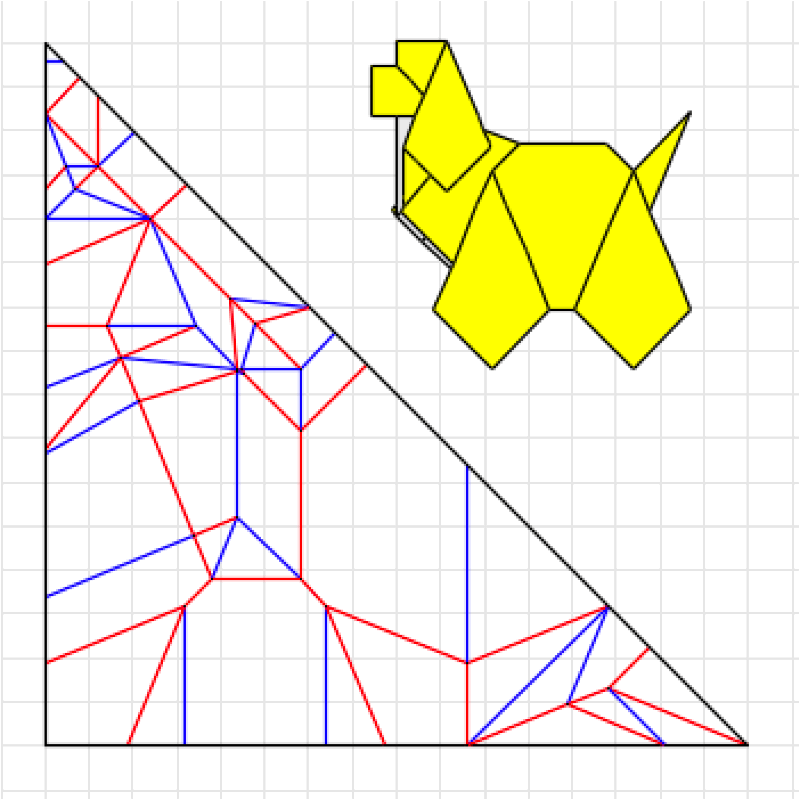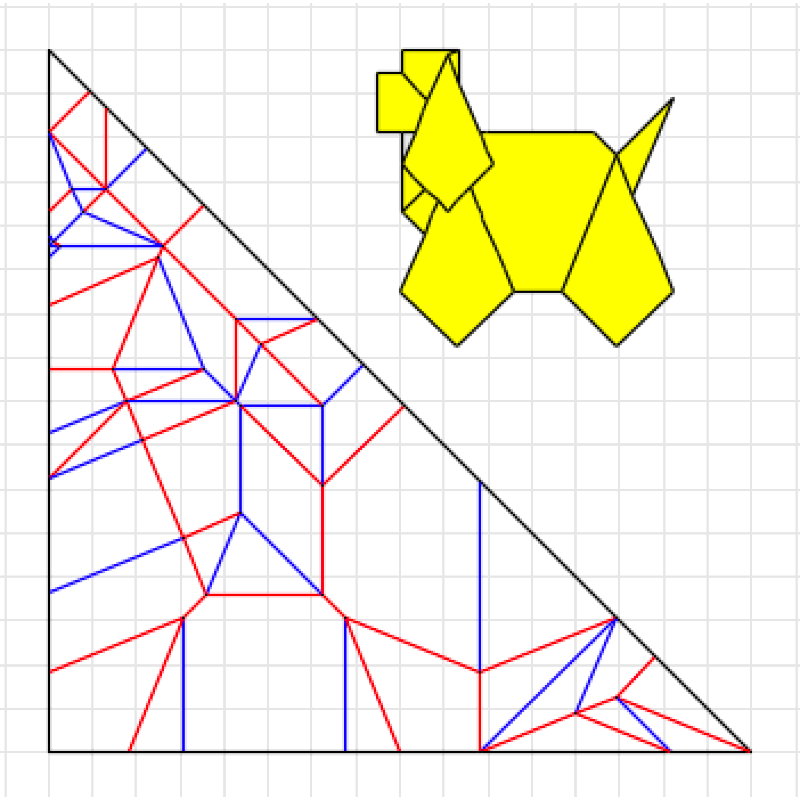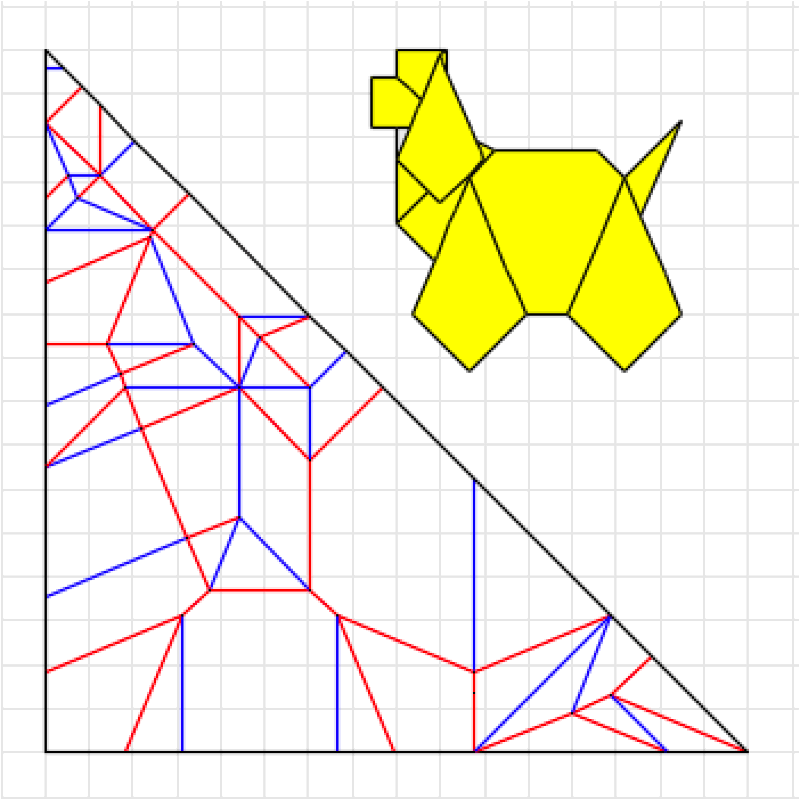
ORIPAやオリヒメで展開図を描きつつ創作を進めていく方法になってから、この連続的変化を意識して煮詰めていくということが多くなった。昔は感覚的にやっていたが、それゆえの見落としがあったと思う。
造形バランスを吟味して、一度Twitterでかなり込み入った比率のものを発表したのだが、この後折り図を制作する段階で思い直して、折り出しやすい比率(それでも作図的な折りが必要だが)に変更した。
微妙な差ではあるが、前の方が若干頭の位置が高くなる。実際に飼っている愛好家から見たらどうなのかは分からないが、ぼくとしてはbeforeの方が造形的にはベターに見える。構造・工程としてはもちろんafterに軍配が上がる。

〜〜〜〜〜〜〜〜〜〜〜〜〜
最後にお知らせです。5月8日(土)に開かれる折紙探偵団東京友の会のオンライン例会で本作を講習します。参加にはオンライン例会のシーズンパスポート(1000円)が必要となり、その発行には申し込みから数日かかるので、もし今からでも参加希望の方がいらしたら早めの手続きをお願いします。詳しくは日本折紙学会のウェブサイトをご覧ください。
origami.jp
市間いおり新曲「School Origami Life!」
今度はアップテンポの曲で、映像と音を完全同期させてキャラクターアニメーションをやってみたいなと、曲のBPMを150にして作曲するところから始めた。30fpsの映像だと1拍が12フレームとキリがよくなって映像を合わせやすくなるのだ。
とりあえずサビから作ったところ、自分ではなかなかキャッチーなんじゃないかという出来にはなったのだが、それに見合うAメロを作るのに苦労する羽目になった。1回ボツにして妥協しつつ今の形に。ミックスのためにプラグインを追加したりいろいろ試してみたけど省略。
School Origami Life!
授業中 ノートの端をつまみ折り
自然と指が動いて Open sink!
放課後はクラブで折り図の続き折るんだ
60工程 指慣らしね
帰宅中 電車で紙を取り出して
人目もはばからずに Origami time!
宿題を終えたら 次の折り図を折るんだ
120工程 折り切れるかな
折って折って折って折ってやっぱ
折って折って折って折ってずっと
折って折って折って折ってもっと
折りまくるのだ
やっぱ折ってやっぱ折ってやっぱ
ずっと折ってずっと折ってずっと
もっと折ってもっと折ってもっと
折りまくるのだ
授業中 ノートの端を沈め折り
当てられそうになって Open out!
週末は徹折り 大作折り図折るんだ
300工程 折り通すのだ
折って折って折って折ってやっぱ
折って折って折って折ってずっと
折って折って折って折ってもっと
折りまくるのだ
やっぱ折ってやっぱ折ってやっぱ
ずっと折ってずっと折ってずっと
もっと折ってもっと折ってもっと
折りまくるのだ
折りまくるのだ!
歌詞は、(自分を含め)最近あんまり折ってないなあという人をTwitterで見かけることがよくあって、折り紙にあけくれる生徒を題材にすることで、かつてのモチベーションに思いを馳せようという発想から。ノートの端を折ったり電車で折ったりのくだりは実体験に基づくが、(時代的に)折り紙クラブの所属経験はない。
アニメの方は、先ほども書いたとおり12フレームの区切りをベースにモーショングラフィックのキーフレームを打っていく。今までのキャライラストを動かすのは大変なので、デフォルメキャラとしたが、こういったちびキャラは一度描いてみたかったので良い機会だった。
モーショングラフィックも全く知識がない状態からだったが、YouTubeの解説動画などを参考にしたら簡単なものなら案外作れるものだ。20代は作画マニア(アニメの動きやそれを描いた原画マンなどに注目してアニメを鑑賞するマイナーな人たち)の周辺をかじっていたのだけど、動きの仕組みなどの基礎的な部分を理解していたのがこんなところで役立った。逆に、目ばかり肥えているせいで自己満足に至れない悲しさもあるけれど。
振り返って、曲のアレンジはちょっと不得意なところに手を伸ばそうとしたために途中からツラい感じだったけど、ループアニメの構想を考えているときはとても楽しかった。ちまちまと進めていたらとっかかりから2ヶ月半もかかってしまって歌詞のテーマと逆行している気もするが、ひとまず作り切れたので良しとしたい。
最後に誰得の「サビだけ30分耐久バージョン」。
www.youtube.com

